Bài tập – Ứng dụng kinh tế vi mô

Bài tập – Ứng dụng kinh tế vi mô có ứng dụng rộng rãi, các dạng ứng dụng sẽ được nêu trong bài viết này:

Bài tập – Ứng dụng kinh tế vi mô 1:

Hàm số cầu của hàng hoá X có dạng: Q_d = 100 – 2P. Mức giá hiện hành là P = 40. Để tăng doanh thu doanh nghiệp cần phải tăng hay giảm giá bán? vì sao?

Ta có hàm cầu của hàng hoá X:

Q_d = 100 – 2P

Tại mức giá hiện hành P = 40, lượng cầu là:

Q = 100 – 2.40 = 20

Doanh thu của doanh nghiệp được xác định bằng:

TR = P.Q = 40.20 = 800

Để xác định doanh nghiệp nên tăng hay giảm giá bán nhằm tăng doanh thu, ta xét mối quan hệ giữa giá và doanh thu. Hàm cầu là hàm tuyến tính nên doanh thu đạt mức tối đa tại điểm giữa của đường cầu. Giá chặn trên của đường cầu được xác định khi Q = 0 :

100 – 2P = 0 <=> P = 50

Như vậy, mức giá tối đa hóa doanh thu là:

P = 50/2 = 25

So sánh với mức giá hiện hành, ta thấy:

P_{Hiện hành} = 40 > P_{Tối ưu} = 25

Điều này cho thấy tại mức giá hiện hành, cầu đối với hàng hóa X là co giãn theo giá. Trong trường hợp cầu co giãn, việc giảm giá sẽ làm lượng cầu tăng với tỷ lệ lớn hơn mức giảm của giá, từ đó làm doanh thu tăng lên.

Bài tập – Ứng dụng kinh tế vi mô 2:

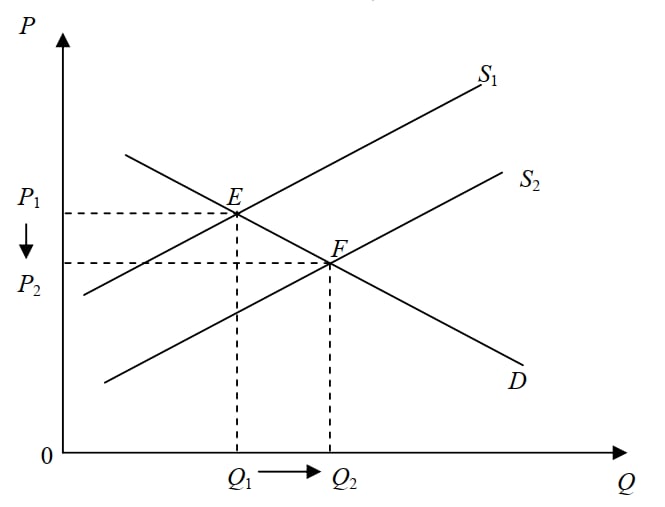
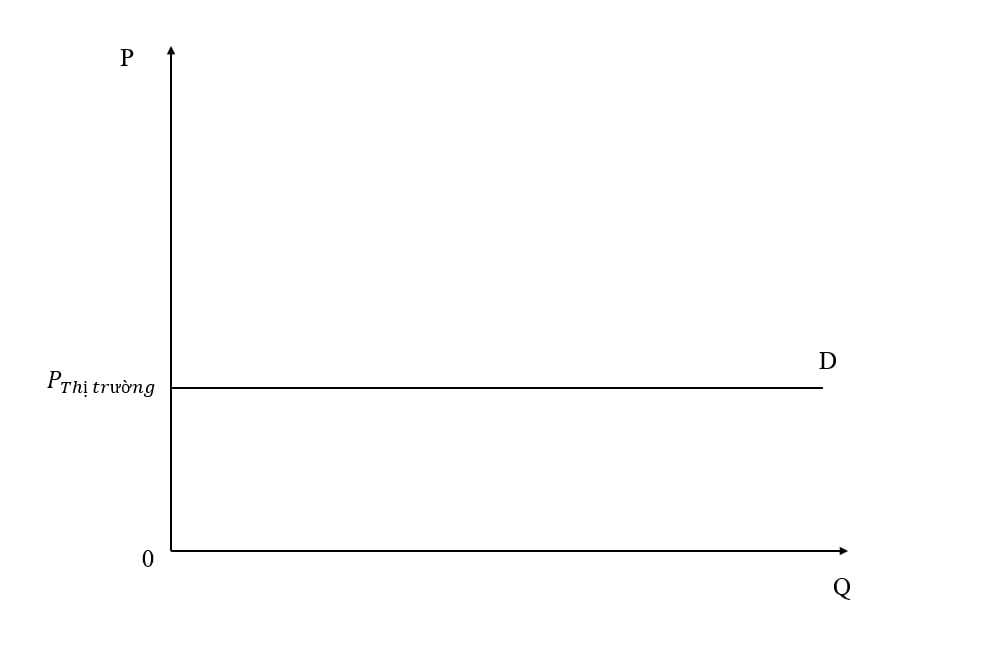
Thị trường sản phẩm Y là thị trường cạnh tranh hoàn hảo. Giá cả và sản lượng cân bằng là P₀ = 20.000đ/sản phẩm; Q₀ = 100.000 sản phẩm. Hệ số co dãn của cầu và cung tại điểm cân bằng là   E_d = 1,6; E_s = 0,4.

1. Xác định hàm số cầu và hàm số cung thị trường (giả thiết đường cầu và đường cung là đường thẳng).

2. Nếu chính phủ đánh thuế thì ai chịu thuế nhiều hơn? Tại sao?

Giải

1. Ta có giá và sản lượng cân bằng là: P₀ = 20.000, Q₀ = 100.000

Vì đường cầu và cung theo giả thiết là đường thẳng và độ co giãn được đo tại điểm cân bằng.

Xác định hàm cầu:

Đường cầu được viết như sau:

Q_d = a – bP

Trong độ co giãn của cầu theo giá được viết như sau:

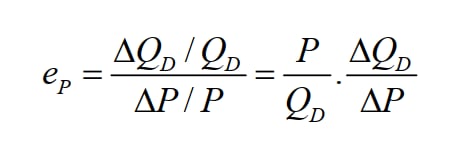
Với hàm tuyến tính:

Từ công thức trên ta rút ra được:

                                          <=> (-1,6) x (100.000/20.000)

                                          <=> -8

=> Hệ số góc đường cầu (b) = – 8

Thay điểm cân bằng vào hàm số đường cầu

                   100.000 = a – 8 x 20.000

=>                          a = 260.000

=> Hàm cầu được vết như sau:

Q_d = 260.000 – 8P

Xác định hàm cung

Hàm cung được viết như sau:

   Q_s = c + d.P

Độ co giãn của cung theo giá được biểu diễn:

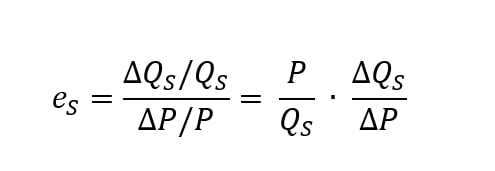
Từ công thức trên rút ra được:

                                     <=> 0,4 x (100.000/20.000)

                                     <=> 2

Thay vào phương trình hàm cung:

                                       100.000 = c + 2 x 20.000

                                             => c = 60.000

Hàm cung được vết như sau:

Q_s = 60.000 + 2P

2. Khi độ co giãn của cầu lớn hơn một cách tương đối so với cung, gánh nặng thuế rơi vào người sản xuất là chủ yếu và ngược lại

Trong bài tập, vì Es = 0,4 < |Ed| = 1,6, cung kém co giãn hơn cầu, vậy bên có độ co giãn nhỏ hơn sẽ chịu gánh nặng thuế lớn hơn.

Bài tập – Ứng dụng kinh tế vi mô 3:

Doanh nghiệp độc quyền hoàn toàn có hàm cầu P = 120 – 2Q, hàm tổng chi phí TC = 3Q² + 20Q + 230.

a. Xác định sản lượng và giá bán tối đa hoá lợi nhuận của doanh nghiệp độc quyền hoàn toàn.

b. Tính lợi nhuận của doanh nghiệp

Giải

a. 

Doanh thu: 

TR = P x Q = (120 − 2Q) x Q = 120Q − 2Q²

Doanh thu cận biên:

                                                                              = 120 – 4Q

Chi phí cận biên:

                                                                               = 6Q + 20

Để tối đa hoá lợi nhuận, doanh nghiệp phải sản xuất sao cho ở đơn vị cuối dùng, Doanh thu biên bằng chi phí biên

MR = MC

120 – 4Q = 6Q + 20

120 – 20 = 6Q + 4Q

100 = 10Q => Q* = 10

Thay vào hàm cầu:

P* = 120 – 2 x 10 = 100

=> Vậy: Sản lượng tối ưu là Q* = 10. Giá bán tối ưu là P* = 100

b.

Lợi nhuận của doanh nghiệp

Tổng doanh thu:

TR = P x Q = 100 x 10 = 1.000

Tổng chi phí:

TC = 3(10)² + 20 x (10) + 230 = 730

Lợi nhuận doanh nghiệp:

π = TR – TC = 1.000 – 730 = 270

Bài tập – Ứng dụng kinh tế vi mô 4:

Một doanh nghiệp cạnh tranh hoàn hảo có tổng chi phí ngắn hạn phụ thuộc vào sản lượng sản xuất và được thể hiện bởi phương trình: TC = 2q³ – 10q² + 200q + 5.000

1. Hãy xác định các hàm: chi phí trung bình (ATC), chi phí biến đổi trung bình (AVC) và chi phí biên (MC) của doanh nghiệp này?
2. Doanh nghiệp sẽ sản xuất ở mức sản lượng nào và lợi nhuận đạt được là bao nhiêu nếu giá thị trường của sản phẩm là 954 (đồng/sản phẩm)?
3. Nếu giá sản phẩm hạ xuống chỉ còn 424 (đồng/sản phẩm) thì doanh nghiệp có sản xuất không? Tại sao? Nếu sản xuất thì doanh nghiệp sẽ sản xuất ở mức sản lượng nào? Lợi nhuận là bao nhiêu?

Giải

Hàm tổng chi phí ngắn hạn:

TC = 2q³ – 10q² + 200q + 5.000

Trong đó:9

200q là chi phí biến đổi (VC)

5.000 là chi phí cố định (TFC)

Câu 1:

Chi phí trung bình (ATC)

ATC = TC/q

<=> ATC = 2q² – 10q + 200 + (5.000/q)

Chi phí biến đổi trung bình (AVC)

AVC = TVC/q

<=> AVC = 2q² – 10q + 200

Chi phí biên (MC)

MC = dTC / dq

<=> MC = 6q² – 20q + 200

Câu 2:

Doanh nghệp cạnh tranh hoàn hảo tối đa hoá lợi nhuận khi 

P = MC (và P ≥ AVC)

Sản lượng tối ưu

954 = 6q² – 20q + 200

<=> 6q² – 20q – 754 = 0

<=> q ≈ 12,8

Doanh thu:

TR = P x q = 954 x 12,8 ≈ 12,211

Tổng chi phí:

TC = 2(12,8)³ – 10(12,8)² + 200(12,8) + 5.000

Lợi nhuận:

π = TR – TC ≈ 12.211 – 9.411 = 2.800

Câu 3:

Doanh nghiệp tiếp tục sản xuất nếu:

P ≥ AVCmin​

AVC = 2q² – 10q + 200

Lấy đạo hàm:

dAVC/dq = 4q – 10 = 0 => q = 2,5

AVCmin = 2(2,5)² – 10(2,5) + 200 = 187,5

So sánh giá và AVC

P = 424 > AVCmin = 187,5

Doanh nghiệp vẫn sản xuất vì bù đắp được chi phí biến đổi

Xác định sản lượng tối ưu

424 = 6q² – 20q + 200

6q² – 20q – 224 = 0

=> q* ≈ 8,1

Doanh thu

TR = 424 x 8,1 ≈ 3.434

Tổng chi phí:

TC ≈ 5,784

Lợi nhuận

π = 3.434 – 5.784 = -2.350

Như vậy, doanh nghiệp vẫn sản xuất vì P > AVCmin, sản lượng doanh nghiệp sẽ sản xuất ở mức q* ≈ 8,1. Lợi nhuận bị lỗ -2.350 nhưng lỗ ít hơn chi phí cố định (5.000), nên vẫn tối ưu hơn ngừng sản xuất.